madisonsilikon.blogg.se - Archimedes method

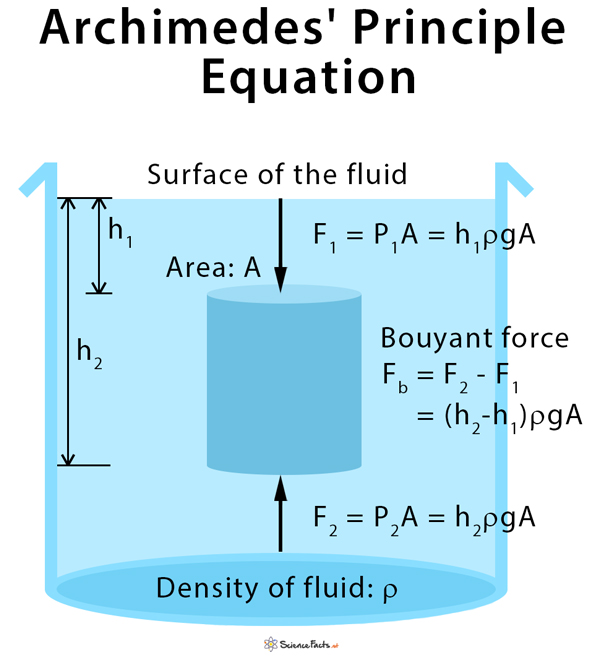
This means that the upward force on the bottom of an object in a fluid is greater than the downward force on the top of the object. (credit: Crystl)Īnswers to all these questions, and many others, are based on the fact that pressure increases with depth in a fluid. (credit: Allied Navy) (c) Helium-filled balloons tug upward on their strings, demonstrating air’s buoyant effect. (b) Submarines have adjustable density (ballast tanks) so that they may float or sink as desired. (a) Even objects that sink, like this anchor, are partly supported by water when submerged. Where does this buoyant force come from? Why is it that some things float and others do not? Do objects that sink get any support at all from the fluid? Is your body buoyed by the atmosphere, or are only helium balloons affected? (See Figure 1.) Figure 1. This is because you no longer have the buoyant support of the water. When you rise from lounging in a warm bath, your arms feel strangely heavy.

Understand the relationship between density and Archimedes’ principle.

Also, the triangle OCD has height r and base CD, so its area is CD r / 2. The area of the circular segment OAB is given by pi r 2 (theta/(2 pi)) = theta r 2 / 2. So the area of OAB must be smaller than the area of OCD. Notice that the circular segment OAB is entirely contained within the triangle OCD. So we now need to show that CD > r * theta. This is the key fact that really uses that we're thinking about circles and not squiggly curves. OK, so by the definition of arc length of a circle, the arc AB = r * theta. If we do that, by breaking our circumscribed polygon up into isosceles triangels, we'll have established the upper bound. We need to prove that the length of the segment CD is longer than the length of the arc AB. I'm on mobile so I can't draw anything, but let me know if you don't understand the setup. Consider a circle with center O, radius r, two points on the circle A and B, angle AOB = theta (which is less than pi), point T on the circle half way along the arc AB, a line L tangent to the circle at T, and then two points C and D which are the intersection of L with the lines continuing OA and OB, respectively. First, notice that the entire proof reduces to the following claim. Let's see if we can prove this using tools he would have had. But obviously Archimedes wasn't working inside that formalism. With modern rigor, we have functions, calculus, and the arc length formula for smooth curves, or even the path length formula in general metric spaces.

How do we measure the length of a curve? Or as Euclid would understand it, how is a curve commensurable with a line? How do they both have well defined "lengths" that can be compared? This is a totally fair objection, but I think it speaks to a more fundamental issue: Your point, I think, is not to claim that the circle actually is squiggly, but rather that it's not clear in the proof where that fact is used, thus calling into question not the correctness of the result but the validity of the proof. This is a better question than the other commenters are giving you credit for. How could Archimedes make this assumption? What if we zoomed into the circle and found that it is a very squiggly line of total length longer than the straight-line perimeter of the circumscribing polygon. What I cannot understand is how one can be sure that the perimeter of the circumscribing polygon is always going to be longer than the circumference of the circle. After all, using the fact that the straight line is the shortest distance between two points, it is easy to prove that the perimeter of the inscribed polygon is always going to be shorter than the circumference of the circle. I can understand how his method provides the lower bound of pi. Finally with a 96-gon he arrived at the conclusion: He then recalculated these bounds by progressively increasing the number of sides of the regular polygons and thus coming closer to an actual value.

This gave him a lower bound and an upper bound for the value of pi. Archimedes worked out the value of pi by calculating the perimeter of a regular polygon inscribed in a circle and the perimeter of a regular polygon circumscribing the same circle.